10304. Оптимальное
бинарное дерево поиска
Рассмотрим множество S = {e1,
e2, …, en} из n различных элементов таких что e1 < e2
< … < en. Построим бинарное дерево поиска для
множества S, в котором чем чаще встречается
элемент, тем ближе он находится к корню.
Стоимость доступа элемента 
в дереве (обозначается
cost(ei)) равно
количеству ребер на пути от корня этого дерева до самого элемента. Если частота
появления элементов S равна {f(e1),
f(e2),
…, f(en)}, то общая стоимость дерева составляет
f(e1) * cost(e1) + f(e2) * cost(e2) + … + f(en) * cost(en)
Дерево поиска с наименьшей общей стоимостью называется
оптимальным бинарным деревом поиска.
Вход.
Каждая строка содержит данные одного теста. Первая строка каждого теста
содержит число n (1 £ n £ 250) – размер множества S. Далее следуют частоты элементов S: f(e1), f(e2),
…, f(en), 0 £ f(ei) £ 100.
Выход. Для каждого теста вывести
стоимость оптимального бинарного дерева
поиска.
Пример входа
1
5
3
10 10 10
3
5 10 20
6 1 3 5 10 20 30
Пример выхода
0
20
20
63
РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Пусть Ti,j равно стоимости оптимального бинарного дерева поиска, которое
можно построить из элементов ei,
ei+1, …, ej. Очевидно, что Ti,i = 0 (стоимость дерева поиска из одной вершины равно нулю).
Для i < j имеет место рекуррентность:
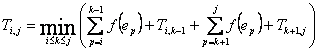
Элемент ek ставим
в корне. Стоимость построения левого поддерева равна 
, правого 
. При этом поскольку корень левого поддерева находится на
один уровень ниже ek, то для учета стоимости левого поддерева
необходимо добавить сумму частот всех его элементов, то есть значение 
. Аналогично при подсчете стоимости правого поддерева следует
прибавить 
.
При i > j
положим Ti,j
= 0.
Отметим также, что решение задачи
про оптимальное бинарное дерево поиска аналогично решению задачи про
оптимальное умножение матриц.
Пример
Рассмотрим множество S, в котором
имеются три элемента e1 < e2 < e3 с частотами 1, 3 и 5. Возможными
деревьями поиска будут:
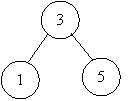
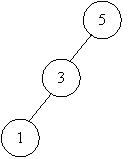
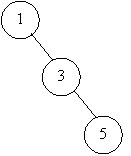
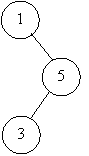
3 + 2 * 5 = 13 5 + 2 * 3 = 11 1 + 5 = 6 3 + 2 * 1 = 5
стоимости деревьев
На рисунках изображены не все
возможные деревья, но отметим, что правое крайнее дерево будет оптимальным, его
стоимость наименьшая среди всех возможных и равна 5.
Рассмотрим четвертый тест.
Искомое оптимальное бинарное дерево поиска имеет вид:
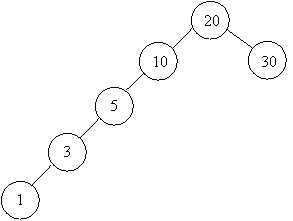
Стоимость левого поддерева (если
бы 10 было корнем): T1,4 = 14.
Стоимость правого поддерева (если
бы 30 было корнем): T6,6 = 0.
Тогда
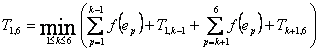
Если при k = 5 достигается указанный минимум, то
= (1 + 3 + 5 + 10) +
14 + (30) + 0 = 63,
что равно стоимости всего дерева.
Реализация алгоритма
Объявим в начале программы следующие макросы:
#define MAX 300
#define
INF 0x3F3F3F3F
Объявим также следующие переменные:
int i, n, m[MAX], sum[MAX];
int t[MAX][MAX];
Входные частоты элементов храним
в массиве m, в массиве sum будут храниться частичные суммы частот: sum[i] = 
. Значения Ti,j будут
раниться в массиве t.
Частичная
сумма 
возвращается функцией
weight(i, j).
int weight(int
i, int j)
{
if (i > j)
return 0;
return sum[j]
- sum[i-1];
}
Функция
go(i, j) возвращает значение Ti,j.
int go(int
i, int j)
{
int k, temp;
if (i > j)
return 0;
if (t[i][j]
== INF)
{
for (k = i;
k <= j; k++)
{
temp = go(i,k-1) + go(k+1,j) +
weight(i,k-1) + weight(k+1,j);
if (temp
< t[i][j]) t[i][j] = temp;
}
}
return
t[i][j];
}
Основная часть программы. При
считывании частот элементов устанавливаем t[i][i] = Ti,i = 0. Остальные значения
ячеек массива t устанавливаем равными бесконечности.
while(scanf("%d",&n)
== 1)
{
memset(t,0x3F,sizeof(t));
for(i = 1; i
<= n; i++)
scanf("%d",&m[i]),
t[i][i] = 0;
Вычисляем частичные суммы массива m.
for(sum[0] =
0, i = 1; i <= n; i++)
sum[i] = sum[i-1] + m[i];
Вычисляем значение T1,n вызовом go(1, n) и печатаем его.
go(1,n);
printf("%d\n",t[1][n]);
}